Custom Firmware, Electronics Design, and PCB Layout

> Lab Book

Buck Switching Converter Design Equations

The buck converter is a high efficiency step-down DC/DC switching converter. The converter uses a transistor switch, typically a MOSFET, to pulse width modulate the voltage into an inductor.  Rectangular pulses of voltage into an inductor result in a triangular current waveform.  We'll derive the various equations for the current and voltage for a buck converter and show the tradeoffs between ripple current and inductance.  For this discussion we assume that the converter is in the continuous mode, meaning that the inductor's current never goes to zero. 

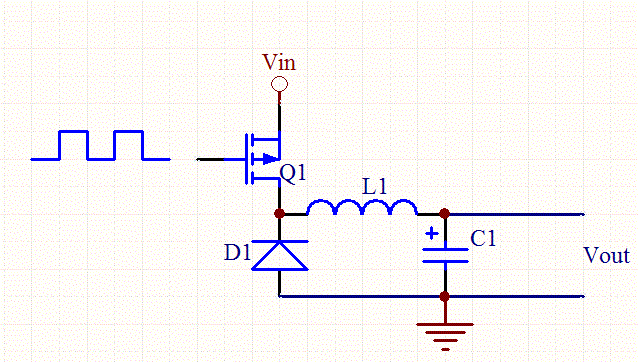
First, here are some definitions:

 

Peak inductor current	ipk
Min inductor current	io
Ripple Current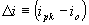
Ripple Current Ratio to Average Current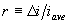
Duty Cycle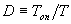
Switch On Time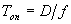
Average and Load Current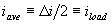
RMS Current for a Triangular Wave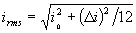

The relationship of voltage and current for an inductor is:

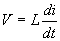   ,or

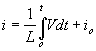
For a constant rectangular pulse:

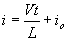
From this we can see that the current is a linear ramp, when the voltage is a constant pulse. 

When the transistor switches on the current is:

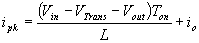, or

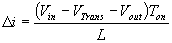Equation 1

and when the transistor switches off the current is:

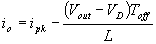, or 

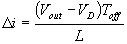
Where V_D  is the voltage drop across the diode, and V_Trans  is the voltage drop across the transistor.  Note that the continuous/discontinuous boundary occurs when i_o is zero. 

By equating through delta i, we can solve for Vout:

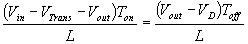
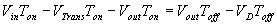
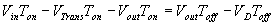
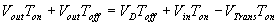
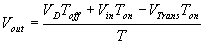
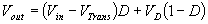
We can also solve for the duty cycle as follows,

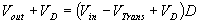
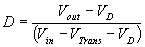
If we neglect the voltage drops across the transistor and diode then:

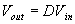
So it is clear that the output voltage is related directly to the duty cycle of the pulses.

The main question when designing a converter is what sort of inductor should be used.   In most designs the input voltage, output voltage and load current are all dictated by the requirements of the design, whereas, the Inductance and ripple current are the only free parameters.  It can be seen form Equation 1, that the inductance is inversely proportional to the ripple current.  In other words,  if you want to reduce the ripple, then use a larger inductor. Thus, in practice a ripple current is decided upon which will give a reasonable inductance.

There are tradeoffs with low and high ripple current.  Large ripple current means that the peak current is i_pk greater, and the greater likelihood of saturation of the inductor, and more stress on the transistor.

So when choosing an inductor make sure that the saturation current of the inductor is greater than i_pk. Likewise, the transistor should be able to handle peak current greater than i_pk. The inductor should also be chosen such that the it can handle the appropriate rms current.

For higher efficiency the diode should be an ultra fast recovery diode. 

These design equations have been incorporated into a convenient Switching Converter Calculator.

Daycounter is a contract electrical engineering company, specializing in electronics and software design.  Please contact us if you need help on your electronics design.

[Employment] [Downloads][Articles] [Contact Us]

Call us now at 801-523-8444  -  136 E. Steep Mountain Dr. Draper, UT 84020

© Copyright 2004 Daycounter, Inc.  All rights Reserved.