Asymmetrical Stepper Motor Ramps
By Tim Daycounter
Most stepper drivers use a trapezoidal acceleration method, with a linearly increasing speed ramp up to the target speed, and a linearly decreasing speed ramp to stop. Normally the trapezoid is symmetrical with starting and ending acceleration ramps that are equal in length. It is possible to use asymmetrical ramps, but the math becomes more complex, especially for the case when the ramp up never reaches the maximum speed, for example when there distance traveled is very short.This article, derives the equations for the ramp lengths in steps for when the length of the ramps in step counts exceeds the total distance that needs to be traveled.
Definitions:
St: The target number of steps to travel, i.e. the total step count.
Sd: The difference between the target number of steps and the sum of the ramps steps.
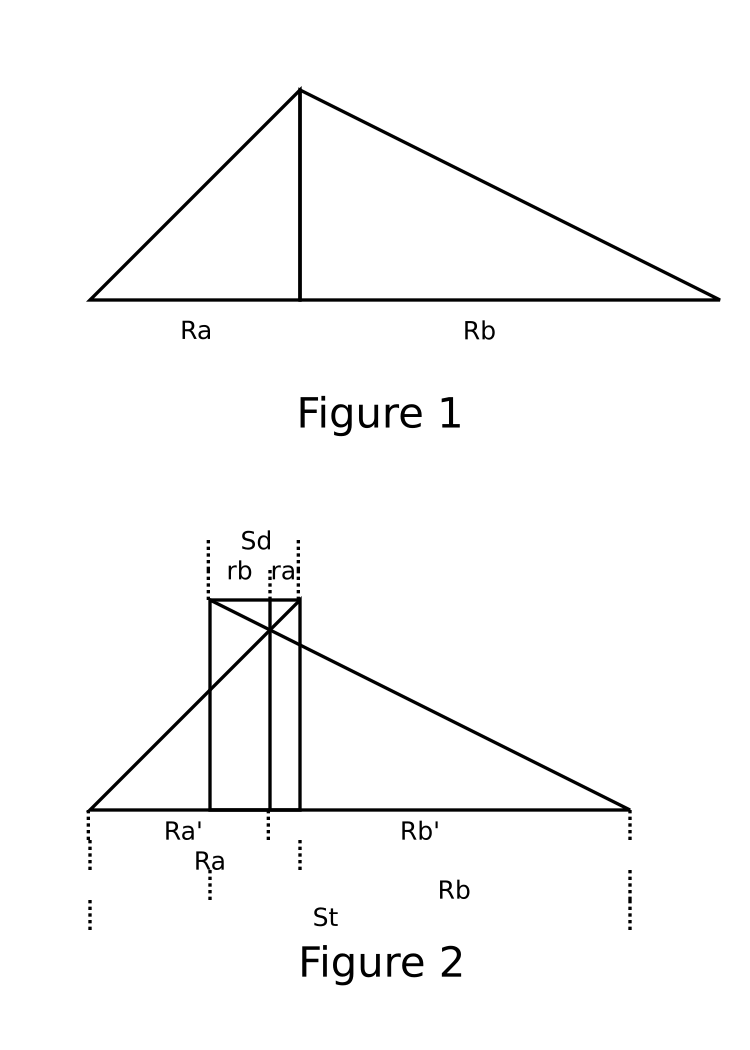
Ra: The starting ramp length in steps when max speed is reached.
Rb: The ending length ramp in steps, when max speed is reached.
Ra': The starting ramp length in steps when less than the max speed is reached.
Rb': The ending length ramp in steps, when less than the max speed is reached.
The goal is to find Ra' and Rb' given St.
For the symmetrical case, it is easy to find Ra' and Rb' because they are merely St/2.
If the ramp up and ramp down lengths equal the
target number of steps,
then the trapezoid degenerates into a triangle, with height equal to
the maximum motor speed. See Figure 1.
If the ramp up and ramp down lengths are less than the target
number of steps,
then the trapezoid degenerates into a triangle, with height less
than the maximum motor speed. See Figure 1.
The upper and low triangles of Figure 2 are proportional so Ra'/St = ra/Sd, and Rb'/St= Rb/Sd.
Sd= ra+rb = [(Ra+Rb)-St]St= Ra'+Rb'
| ra/Sd= RA/(Ra+Rb) | rb/Sd= RB/(Ra+Rb) |
| ra= RA*Sd/(Ra+Rb) | rb= RB*Sd/(Ra+Rb) |
| ra= RA/(Ra+Rb)* [(Ra+Rb)-St] | ra= RA/(Ra+Rb)* [(Ra+Rb)-St] |
| Ra'= Ra-ra | Rb'= Rb-rb |
| Ra'= Ra - RA/(Ra+Rb)* [(Ra+Rb)-St] | Ra'= Ra - RA/(Ra+Rb)* [(Ra+Rb)-St] |
It is computationally more efficient to calculate Ra' from the formula above, and then subtract it from the total step count St. If you are using integer arithmetic, this method will guarantee that no steps are lost from integer round down.

