Sallen-Key Low Pass Butterworth Filter Calculator
This calculator calculates the capacitor values For a Sallen-Key low pass Butterworth, Bessel, and Chebyshev filters.
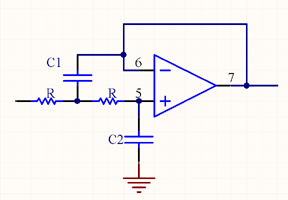
The Sallen-Key filter is a simple active filter based on op-amps stages, which is ideal for filtering audio frequencies.
The calculator only computes filters that have an even number of poles, which is a more efficient use off op-amps. Odd order filters require a single extra real pole which still requires an op-amp, so it makes sense to just use a higher order even filter. For example, if an application requires a third order filter requiring 2 op-amps, it makes more sense to use a forth order filter, which also requires 2 op-amps.
For a derivation of the design equations see this link:
Low Pass Sallen-Key Design Equations
| Bessel Normalization Factors | |
| Order, n | Factor |
| 1 | 1 |
| 2 | 1.36 |
| 3 | 1.75 |
| 4 | 2.13 |
| 5 | 2.42 |
| 6 | 2.7 |
| 7 | 2.95 |
| 8 | 3.17 |
| 9 | 3.39 |
| 10 | 3.58 |
For Bessel functions the natural frequency is the where the delay is 1 second, rather than 3dB point. In addition, this natural frequency is different for each order. The response can be normalized to the 3dB cut off point for each order of filter, by the normalization factors in the above table. Note that the delay is also scaled by the factor as well. For example for a normalized 3rd order filter, the delay at the 3db frequency is 1sec/1.75 rather than 1sec.
To use this calculator, select a resistance, the number of poles, and the cut-off frequency.
Note that the filters are normalized to the 3db cut off point, which is not necessarily the natural frequency.

